And x>y mathematics Pick a twodigit number greater than 25 Rewrite your twodigit number as a difference of two numbersX and y are positive integers;For example, see x4 y4 as (x2)2 (y 2 ) 2 , thus recognizing it as a difference of squares that can be factored as (x 2 y 2 )(x 2 y 2 ) Factoring out a monomial from a polynomial Univariate
3
The identity (x^2 y^2)^2=(x^2-y^2)^2 (2xy)^2 can be used to generate pythagorean triples
The identity (x^2 y^2)^2=(x^2-y^2)^2 (2xy)^2 can be used to generate pythagorean triples-For example, the polynomial identity (x 2 y 2) 2 = (x 2 – y 2) 2 (2xy) 2 can be used to generate Pythagorean triples Rewrite rational expressions AAPRD62 Define appropriate quantities for the purpose of descriptive modeling (Shared with AI) PARCC This standard will be assessed in Algebra (involving Algebra II content or securely held content from previous grades and courses) require the student to create a quantity of interest in the situation being described (ie,



Http Citeseerx Ist Psu Edu Viewdoc Download Doi 10 1 1 139 8042 Rep Rep1 Type Pdf
The answers to estudyassistantcomWrite a(x)/ b(x) in the form q(x) r(x)/ b(x), where a(x), b(x), q(x), and r(x) are polynomials with the degreeStudents will prove the polynomial identity ( x^2 y^2 )^2 ( 2xy )^2 = ( x^2 y^2 )^2 and use it to generate Pythagorean triplesUse this activity as independent/partner practice or implement it as guided notes and practice for students in need of extra supportThis activity is in PDF formatPar
For example, the polynomial identity (x 2 y 2) 2 = (x 2 – y 2) 2 (2xy) 2 can be used to generate Pythagorean triples AIIAAPRC5 () Know and apply the Binomial Theorem for the expansion of (x y) n in powers of x and y for a positive integer n, where x and y are any numbers, with coefficients determined for example by Pascal'sWrite a(x)/ b(x) in the form q(x) r(x)/ b(x), where a(x), b(x), q(x), and r(x) are polynomials with the degree of r(x) lessStudents will prove the polynomial identity ( x^2 y^2 )^2 ( 2xy )^2 = ( x^2 y^2 )^2 and use it to generate Pythagorean triples Use this activity as independent/partner practice or implement it as guided notes and practice for students in need of extra support
For example, the polynomial identity (x 2 y2)2 = (x2 – y2)2 (2xy)2 can be used to generate Pythagorean triples 5 () Know and apply the Binomial Theorem for the expansion of (x y)n in powers of x and y for a positive integer n, where x and y are any numbers, with coefficients determined for example by Pascal's Triangle Rewrite CCSSMathContentHSAAPRC4 Prove polynomial identities and use them to describe numerical relationships For example, the polynomial identity (x 2 y 2) 2 = (x 2 y 2) 2 (2xy) 2 can be used to generate Pythagorean triples Authors National Governors Association Center for Best Practices, Council of Chief State School OfficersFor example, the polynomial identity (x 2 y 2) 2 = (x 2 y 2) 2 (2xy) 2 can be used to generate Pythagorean triples CCSSMathContentHSAAPRC5 () Know and apply the Binomial Theorem for the expansion of ( x y ) n in powers of x and y for a positive integer n , where x and y are any numbers, with coefficients determined for example




A Apr 4 Objective Adding Amp Subtracting Polynomials Prove Polynomial Identities And Use Them



2
2 n A expressions are the expectatio Use the structure of an expression to identify ways to rewrite it For example, see x4 – y4 as (x2)2 – (y2)2, thus recognizing it as a difference of squares that can be factored as (x2 – y2)( x2 y2) Polynomial and rational ns at this level Understand the relationship between zeros and factors ofIdentity (x^2 y^2)^2 = (x^2 y^2)^2 (2xy)^2 can be used to generate Pythagorean triples The Binomial Theorem AAPR5 () Know and apply the Binomial Theorem for the expansion of (x y)^n in powers of x and y for a positive integer n, where x and y are any numbers, with coefficients determined for example by Pascal's TriangleHSASSE Use the structure of an expression to identify ways to rewrite it For example, see x^4 y^4 as (x^2)^2 (y^2)^2, thus recognizing it as a difference of squares that can be factored as (x^2 y^2)(x^2 y^2)




Understanding Pythagorean Identities Studypug




Pythagorean Theorem An Overview Sciencedirect Topics
PreAlgebra Simplify (2xy^22x^3x^2y) (2x^2y2xy^2y^3) (2xy2 2x3 − x2y) − (−2x2y 2xy2 − y3) ( 2 x y 2 2 x 3 x 2 y) ( 2 x 2 y 2 x y 2 y 3) Simplify each term Tap for more steps Apply the distributive property Use the identity (x2y2)2=(x2−y2)2(2xy)2 to determine the sum of the squares of two numbers if the difference of the squares of the numbers is 5 and the product of the numbers is 6 Enter your answer as a number, like this 42For example, the polynomial identity (x2 y2)2 = (x2 – y2)2 (2xy)2 can be used to generate Pythagorean triples Rewrite rational expressions NCM3AAPR6 Rewrite simple rational expressions in different forms;




Aim How Do We Use Structure To Prove Find Pythagorean Triples Ppt Download
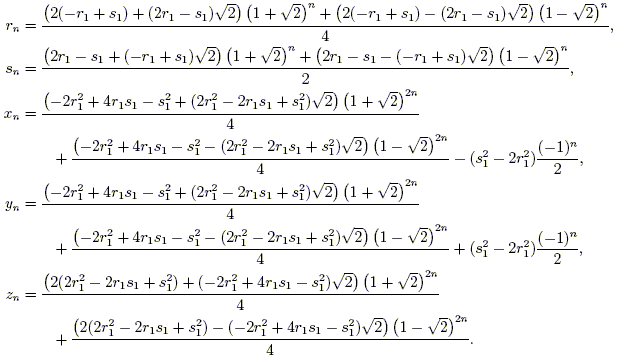



Pythagorean Triples
MGSE912AAPR4 Prove polynomial identities and use them to describe numerical relationships For example, the polynomial identity (x^2 y^2)^2 = (x^2 – y^2)^2 (2xy)^2 can be used to generate Pythagorean triples Video Lessons ( p1, p2a,For example, the polynomial identity (x^2 y^2 )^ 2 = (x^2 – y^ 2 )^ 2 (2xy)^2 can be used to generate Pythagorean triples AAPRC5 () Know and apply the Binomial Theorem for the expansion of (x y)^n in powers of x and y for a positive integer n, where x and y are any numbers, with coefficients determined for example by Pascal's Triangle 👍 Correct answer to the question The identity (x^2 y^2)^2 = (x^2 y^2)^2 (2xy)^2 can be used to generate Pythagorean triples What Pythagorean triple could be generated using x = 8 and y = 3?




Facilitator David Brown Ppt Download




Pythagorean Theorem Wikipedia
4 Prove polynomial identities and use them to describe numerical relationships For example, the polynomial identity (x 2 y 2) 2 = (x 2 – y 2) 2 (2xy) 2 can be used to generate Pythagorean triples With the increase in technology and this huge new thing called the Internet, identity theft has become a worldwide problemFor example, the polynomial identity (x 2 y 2) 2 = (x 2 – y 2) 2 (2xy) 2 can be used to generate Pythagorean triples Suggested Learning Targets Understand that polynomial identities include but are not limited to the product of the sum and difference of two terms, the difference of two squares, the sum and difference of two cubes, theAAPRC4 Prove polynomial identities and use them to describe numerical relationships For example, the polynomial identity (x2 y2)2 = (x2 – y2)2 (2xy)2 can be used to generate Pythagorean triples



Recognize Patterns That Make Pythagorean Triples Learnzillion
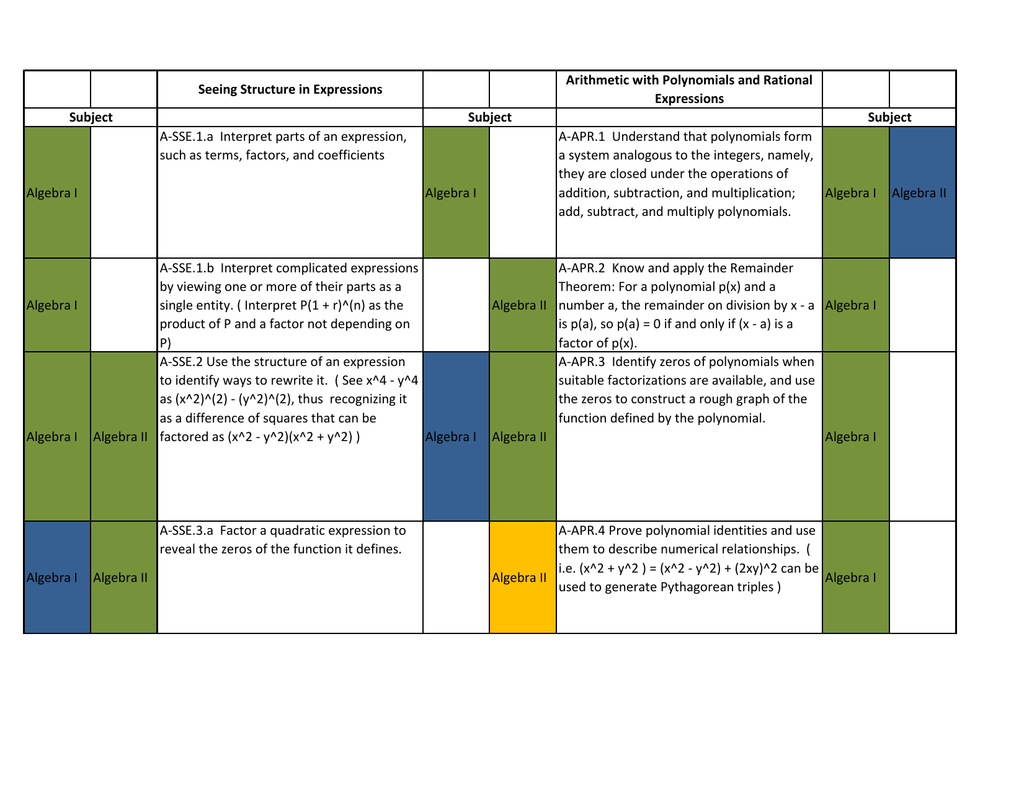



Seeing Structure In Expressions Arithmetic With Polynomials And
Generate Pythagorean Triples using an identity You'll gain access to interventions, extensions, task implementation guides, and more for this instructional video In this lesson you will learn to generate a Pythagorean Triple by using the identity (x^2 y^2)^2 (2xy)^2 = (x^2 y^2)^2And x>y (x2−y2)2(2xy)2=(x2y2)2 If the sides of a right triangle are 57, 176, and 185, what are the values of x and y?• See x4 – y4 as (x2)2 – (y2)2, thus recognizing it as a difference of squares that can be factored as (x2 – y2)(x2 y2) • In the equation x2 2x 1 y2 = 9, see an opportunity to rewrite the first three terms as (x1)2, thus recognizing the equation of a circle with radius 3 and center (−1, 0)



2



Arxiv Org Pdf 1902
What is the new area of the square?Use the identity (x y) 2 = x 2 2xy y 2 and use x = x and y = 2 Answer (x 2) 2 2 can be used to generate Pythagorean triples Standard Staircase Grade 6 Creating Equivalent Expressions By (date), when For example, the polynomial identity (x 2 y 2) 2 = (x 2 – y 2) 2 (2xy) 2 can be usedGraph x^2y^22x2y1=0 Find the standard form of the hyperbola Tap for more steps Add to both sides of the equation Complete the square for The second focus of a hyperbola can be found by subtracting from Substitute the known values of , , and into the formula and simplify The foci of a hyperbola follow the form of




Aim How Do We Use Structure To Prove Find Pythagorean Triples Ppt Download



2
For example, the polynomial identity (x 2 y 2) 2 = (x 2 y 2) 2 (2xy) 2 can be used to generate Pythagorean triples CCSSMathContentHSAAPRC5 () Know and apply the Binomial Theorem for the expansion of ( x y ) n in powers of x and y for a positive integer n , where x and y are any numbers, with coefficients determined for exampleFor example, the polynomial identity (x2 y2)2 = (x2 y2)2 (2xy)2 can be used to generate Pythagorean triples AAPRD Rewrite rational expressions AAPRD6 Rewrite simple rational expressions in different forms; The following identity can be used to find Pythagorean triples, where the expressions x2−y2, 2xy, and x2y2 represent the lengths of three sides of a right triangle;



Recognize Patterns That Make Pythagorean Triples Learnzillion



Pythagorean Identities Mathbitsnotebook Ccss Math
Example, the polynomial identity (x2 y2) 2 = (x2 – y 2) 2 (2xy)2 can be used to generate Pythagorean triples 8) AAPR6 Rewrite simple rational expressions in different forms; The identity (x^2 y^2)^2 = (x^2 y^2)^2 (2xy)^2 can be used to generate Pythagorean triples What Pythagorean triple could be generated using x = 8 2376X and y are positive integers;




Pythagorean Triple From Wolfram Mathworld



Http Www Admschools Org Wp Content Uploads 15 10 12 05 May 14 12 07 Pdf
Identity (x2y2)2 = (x2– y2)2 (2xy)2 can be used to generate Pythagorean triples HSMP7 Look for and make use of structure HSMP8 Look for and express regularity in repeated reasoning AAPR4 Understand that polynomial identities include but are not difference of two squares, the sum and difference of two cubes, the square of aCCSSMathContentHSAAPRC4 Prove polynomial identities and use them to describe numerical relationships For example, the polynomial identity (x 2 y 2) 2 = (x 2 y 2) 2 (2xy) 2 can be used to generate Pythagorean triples Authors National Governors Association Center for Best Practices, Council of Chief State School OfficersFor example, the polynomial identity (x^2 y^2)^2 = (x^2 – y^2)^2 (2xy)^2 can be used to generate Pythagorean triples I can prove polynomial identities



Times Module M15 Pythagoras Theorem




Polynomial Identities And Pythagorean Triples Activity Polynomials Algebra Resources Algebra 2 Activities
Identity (x^2 y^2)^2 = (x^2 – y^2)^2 (2xy)^2 can be used to generate Pythagorean triples A AREI06 Solve systems of equations Solve systems of linear equations exactly and approximately (eg, with graphs), focusing on pairs of linear equations in two variables 22b Solve systems of linear equations andThe polynomial identity (x2 y2)2 = (x2 – y2)2 (2xy)2 can be used to generate Pythagorean triples SE/TE CB 318 AAPR5 () Know and apply the Binomial Theorem for the expansion of (x y)n in powers of x and y for a positive integer n, where x y are any numbers, with coefficients determined for example by Pascal's Triangle SE/TEFor example, the polynomial identity (x 2 y 2) 2 = (x 2 y 2) 2 (2xy) 2 can be used to generate Pythagorean triples HSAAPRC5 () Know and apply the Binomial Theorem for the expansion of (x y) n in powers of x and y for a positive integer n, where x and y are any numbers, with coefficients determined for example by Pascal's Triangle



2




Pythagorean Triple From Wolfram Mathworld
For example, the polynomial identity (x^2 y^2)^2 = (x^2 – y^2)^2 (2xy)^2 can be used to generate Pythagorean triples 5 () Know and apply the Binomial Theorem for the expansion of (x y)^n in powers of x and y for a positive integer n, where x and y are any numbers, with coefficients determined for example by Pascal's Triangle1HSAAPRC4 Prove polynomial identities and use them to describe numerical relationships For example, the polynomial identity $(x^2 y^2)^2 = (x^2 y^2)^2 (2xy)^2$ can be used to generate Pythagorean triplesJMAP STANDARD AAPRC4 AII Prove polynomial identities and use them to describe numerical relationships For example, the polynomial identity (x 2 y 2) 2 = (x 2 –y 2) 2 (2xy) 2 can be used to generate Pythagorean triples WORKSHEETS RegentsPolynomial Identities




Pdf The Modular Tree Of Pythagoras
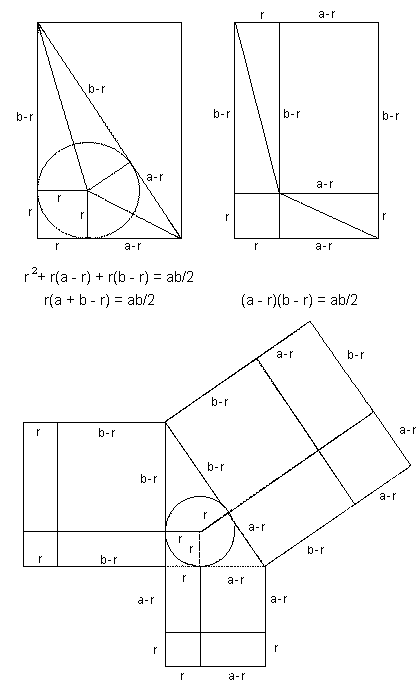



Pythagorean Theorem And Its Many Proofs
Write a(x)/b(x) in the form q(x) r(x)/b(x), where a(x), b(x), q(x), and r(x) are polynomials with the degree of r(x) less than theIdentity (x2 y2)2 = (x2 y2)2 (2xy)2 can be used to generate Pythagorean triples Standard for Mathematical Practices SMP 7 Students look for and make use of structure when given a polynomial function in factored form Students will be able to find the zeros, plot the zeros and then make a sketch of the graph of that is reflective of theFor example, the polynomial identity (x 2 y 2) 2 = (x 2 – y 2) 2 (2xy) 2 can be used to generate Pythagorean triples Interpret functions that arise in applications in terms of the context MGSE912FIF4 Using tables, graphs, and verbal descriptions, interpret the key characteristics of a function which models the relationship



Generating Pythagorean Triples Chilimath



2
4 – y4 as (x2)2 (y2)2, thus recognizing it as a difference of squares that can be factored as (x 2 – y 2 ) (x 2 y 2 ) Use polynomial identities to solve problemsSelect two answers one for x and one for y 15 10 Identities V Last updated at by Teachoo Identity V is (a b c) 2 = a 2 b 2 c 2 2ab 2bc 2ca Let us prove it Proof (a b c) 2 = ( (a b) c) 2 Using (x y) 2 = x 2 y 2 2xy



Www Jstor Org Stable 10 4169 College Math J 48 2 115




How To Use The Pythagorean Theorem With A Circle Veritas Prep
Correct answers 2 question The identity (x^2 y^2)^2 = (x^2 y^2)^2 (2xy)^2 can be used to generate Pythagorean triples What Pythagorean triple Answer 2 📌📌📌 question The identity (x^2 y^2)^2 = (x^2 y^2)^2 (2xy)^2 can be used to generate Pythagorean triples What Pythagorean triple could be generated using x = 8 and y = 3? The following identity can be used to find Pythagorean triples, where the expressions x2−y2, 2xy, and x2y2 represent the lengths of three sides of a right triangle;



Pythagorean Triangles And Triples



Times Module M15 Pythagoras Theorem
For example, the polynomial identity (x 2 y 2) 2 = (x 2 – y 2) 2 (2xy) 2 can be used to generate Pythagorean triples 5 () Know and apply the Binomial Theorem for the expansion of (x y) n in powers of x and y for a positive integer n, where x and y are any numbers, with coefficients determined for example by Pascal's Triangle




Pdf Pythagorean Triples Before And After Pythagoras




Problem Books In Mathematics




Trigonometry 6th Ed Part 2 By Josh Ramirez Issuu



Math Questions Math Answers



Q Tbn And9gctcnkr03soarrf1vsfmhkpwoqgnnut06hftvh9xjniw0r Zsimz Usqp Cau



Pythagorean Triangles And Triples
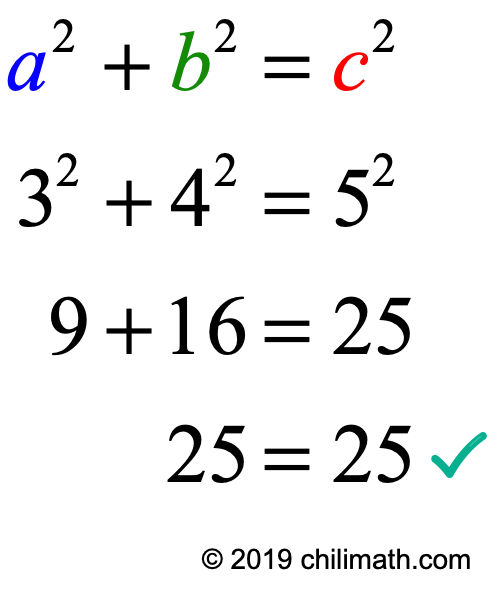



Generating Pythagorean Triples Chilimath




Generate Pythagorean Triples Using An Identity Learnzillion



Http Citeseerx Ist Psu Edu Viewdoc Download Doi 10 1 1 139 8042 Rep Rep1 Type Pdf



Achieve Lausd Net Cms Lib Ca Centricity Domain 244 Curriculum maps Algebra 2 curr map Algebra 2 textbook aligment cpm Pdf




What Are Some Examples Of The Most Common Pythagorean Triples Quora




P O L Y N O M I A L I D E N T I T I E S E X A M P L E S Zonealarm Results




Pythagorean Theorem An Overview Sciencedirect Topics




P O L Y N O M I A L I D E N T I T I E S E X A M P L E S Zonealarm Results




File
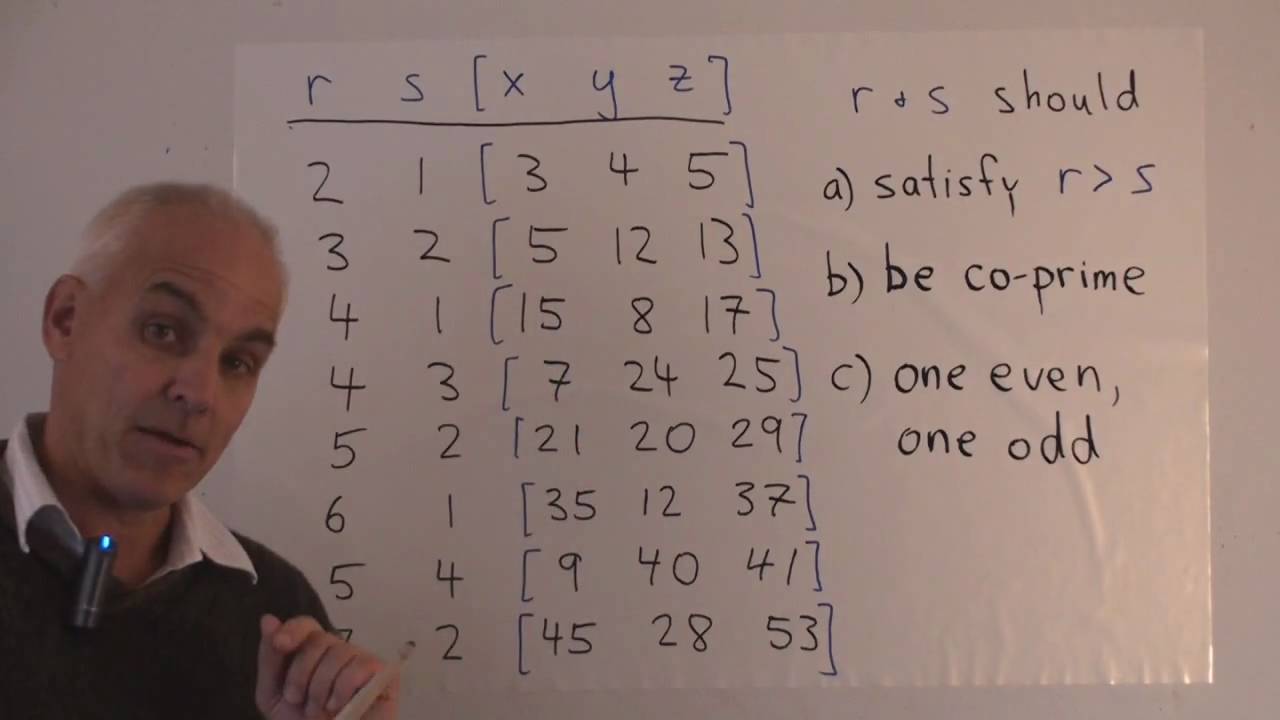



Pythagorean Triples Explanation Examples
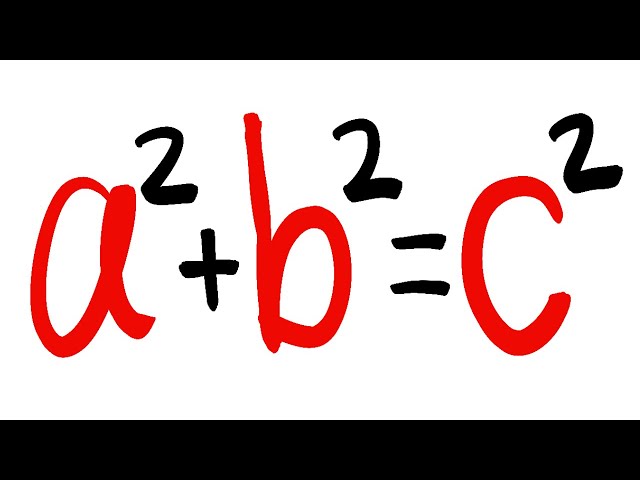



Pythagorean Triples Generator Youtube




The Identity X 2 Y 2 2 X 2 Y 2 2 2xy 2 Can Be Used To Generate Pythagorean Triples What Pythagorean Triple Could Be Generated




Math 22 The Fundamental Theorem Of Arithmetic Lecture R 10 30 Pdf Free Download



Http Lpcsdrpoulsen Weebly Com Uploads 2 4 0 1 9 Key 1 Pdf



Www Maths Ed Ac Uk V1ranick Papers Hatchertn Pdf




Type The Correct Answer In Each Box In Part E You Proved That Any Pythagorean Triple Can Be Brainly Com



2




Aim How Do We Use Structure To Prove Find Pythagorean Triples Ppt Download



Achieve Lausd Net Cms Lib Ca Centricity Domain 244 Curriculum maps Algebra 2 curr map Algebra 2 ccss curriculum map unit 2 draft 8 23 16 Pdf
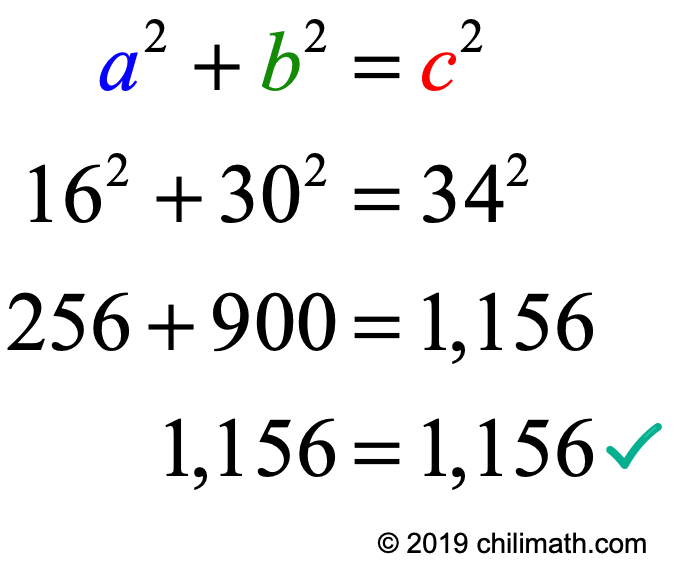



Generating Pythagorean Triples Chilimath



3



2




Aim How Do We Use Structure To Prove Find Pythagorean Triples Ppt Download



Www Engageny Org File Download Algebra Ii M1 Topic A Lesson 10 Teacher Pdf Token H3w7mcpp



Does This Equation Have An Infinite Number Of Rational Solutions Math X 2 Y 2 2 Math Quora



1



Www Georgiastandards Org Georgia Standards Frameworks Acc Geometry B Algebra Ii Comprehensive Course Overview Pdf



Http Www Math Brown Edu Jhs Frintdir Frintch2ch3 Pdf




Pythagorean Theorem How To Use Pythagoras Theorem With Examples




Lesson 10 The Power Of Algebra Finding



Http Www Math Odu Edu Jhh Geometry Pdf




Polynomial Identities Solutions Examples Videos Worksheets Games Activities




Pythagorean Theorem How To Use Pythagoras Theorem With Examples




Pdf Pythagorean Triples Before And After Pythagoras




Pythagorean Triples Video Lessons Examples Step By Step Solutions




Pdf Pythagorean Triples Before And After Pythagoras Ravi Agarwal Academia Edu




Generating Pythagorean Triples Chilimath



Doe Nv Gov Uploadedfiles Nde Doe Nv Gov Content Nevada Academic Standards Math Documents Mathstandards Pdf



1
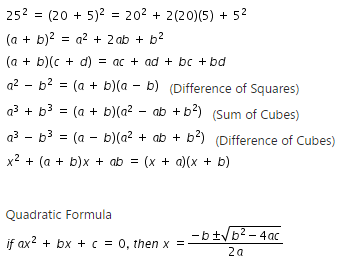



Mafs 912 A Apr 3 4 Prove Polynomial Identities And Use Them To Describe Numerical Relationships For Example The Polynomial Identity X Y X Y 2xy Can Be Used To Generate Pythagorean Triples
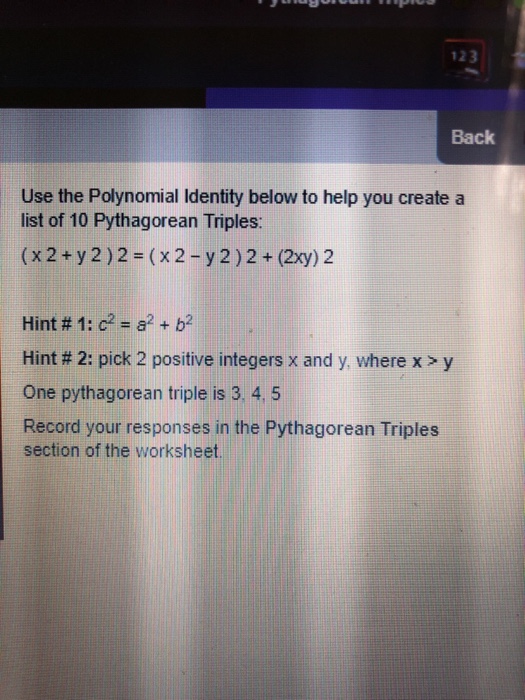



123 Back Use The Polynomial Identity Below To Help Chegg Com




Formulas For Generating Pythagorean Triples Wikipedia



2




U X 2 Y 2 2xy U X 2 Y 2 2xy U X 1 2 Chegg Com




Analyzing Polynomial Identities Video Khan Academy
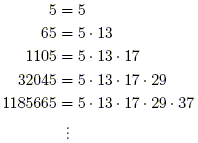



Pythagorean Triples




Pdf Pythagorean Triples Before And After Pythagoras




A Collection Of Algebraic Identities Pi Numbers



Education Ohio Gov Getattachment Topics Learning In Ohio Mathematics Ohio S Learning Standards In Mathematics Algebra 2 Math 3 Standards Pdf Aspx Lang En Us




Use The Pythagorean Identity X2 Y 2 2xy 2 X2 Y2 2 To Create A Pythagorean Brainly Com



2




V Y 2 2xy Y 2 Dx 11 2 2yz 2y Y Chegg Com



Http Www Math Northwestern Edu Mlerma Problem Solving Putnam Training Problems 13 Pdf




How To Use The Pythagorean Theorem With A Circle Veritas Prep




Jason Uses The Polynomial Identity X Y 2 X 2 2xy Y 2 To Show That 6 36 Brainly Com



Www Brewtoncityschools Org Cms Lib Al Centricity Domain 133 8 2 The Pythagorean Theorem And Its Converse Pdf
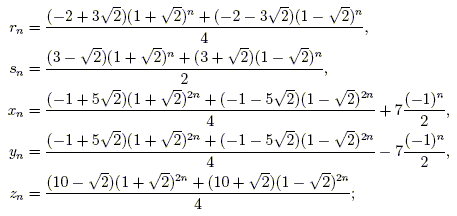



Pythagorean Triples



Pythagorean Triangles And Triples




Answered Example 3 Jeremy Uses The Polynomial Bartleby




Pythagorean Triple From Wolfram Mathworld



2




Pythagorean Triplet In An Array Geeksforgeeks




Formulas For Generating Pythagorean Triples Wikipedia



Pythagorean Triangles And Triples
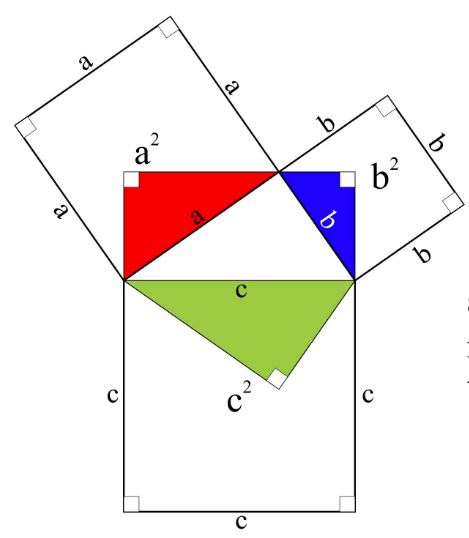



Pythagorean Theorem And Its Many Proofs




Calc3 1001 By James Bardo Issuu




Understanding Pythagorean Identities Studypug




Polynomial Identities Solutions Examples Videos Worksheets Games Activities



0 件のコメント:
コメントを投稿